W poniższym artykule przedstawiono propozycję wykorzystania programów przygotowanych przy pomocy programu Scratch do wspierania aktywnego procesu nauczania i utrwalania wiedzy w zakresie matematyki.
Co to jest aktywizacja
Jak wskazuje Majewicz(2012) słowa „aktywność” oraz „aktywizacja” wywodzą się od tego samego łacińskiego słowa activus oznaczającego czynny. Zatem aktywizacje uczniów można rozumieć jako proces, którego celem jest doprowadzenie do sytuacji, w której uczniowie aktywnie uczestniczą w procesie nauczania i zdobywania nowej wiedzy. Aktywizacja jest też określana jako ogół poczynań nauczyciela i uczniów zapewniających dzieciom odgrywanie czynnej roli w realizacji zadań. Uczniowie uczą się w trakcie własnej aktywności. Chodzi o to, by potrzebną wiedzę i umiejętności nabywali w sposób trwały, skuteczny i przyjemny.
Dlaczego aktywizacja i porównanie
W nauczaniu matematyki często, historycznie stosowane były metody podające, ponieważ dawniej uczenie się polegało prawie wyłącznie na przyswajaniu gotowej wiedzy. Obecnie dydaktyka daje pierwszeństwo metodom problemowym ze szczególnym uwzględnieniem metod aktywizujących. Kładzie się na nacisk na kształtowanie postawy uczniów wobec poznawanych zagadnień. Kluczowa rola takiego podejścia wynika z powiązania z rzeczywistością pozą szkolną, której odkrywania realizuje się przede wszystkim poprzez działanie, a także ze względu na skuteczność (Szeremeta, 1992). Propagatorzy metod aktywizujących zwracają uwagę na samodzielne dochodzenie uczniów do wiedzy, co powoduje, że staje się ona bardziej trwała, a także zaangażowanie w takiej lekcji wszystkich uczniów pogłębia ich zdolności pracy w grupie oraz możliwości analizowania i interpretowanie rzeczywistości. Należy pamiętać, że umiejętności te są kluczowe we współczesnym świecie.
Różnorodność aktywności a mimo to skuteczność
Aktywność uczniów może przejawiać się w odmiennych formach i w różnym nasileniu. Wynika to między innymi z tego, że różne zmysły mogą w mniejszym lub większym stopniu wpływać na przyswajanie wiedzy u konkretnego dziecka. Wyróżnia się wzrokowców, słuchowców i kinestetyków w zależności od tego, czy dominującym zmysłem jest odpowiednio wzrok, słuch lub dotyk oraz czynności ruchowe (Janowicz, 2009). Metody aktywizujące także te zaprezentowane jako konkretne przykłady można uznać za obiektywne, w takim sensie, że dostarczają bodźców do tych trzech dominujących zmysłów. Ponadto niezależnie od sposobu przyswajania informacji przez konkretnego ucznia, metoda przyjęta przez nauczyciela może radykalnie zmienić ilość przyswojonych informacji. W poniższych przykładach zamiast podawać gotowe informacje (uczniowie pamiętają tylko 10% z tego, co słyszą i/lub widzą), nauczyciel zachęca uczniów i daje warunki do bycia odkrywcą i eksperymentatorem, wprowadzenie atrakcyjnych środków dydaktycznych działających na wzrok powoduje już wzrost zapamiętywania informacji do 20%. Idąc dalej umożliwienie uczniom możliwości rozmowy i dyskusji, o swoich programach, zwiększa ilość zapamiętywanej informacji do 40%. Na koniec umożliwienie uczniom uczenia się poprzez działanie, opracowanie własnego programu, powoduje iż zapamiętują 90% tego, co robią.
Narzędzia informatyczne
Poniższe przekłady stanowią propozycję wykorzystanie narzędzi informatycznych do rozwiania u uczniów umiejętności matematycznych. Rozwiazywanie problemu z wykorzystaniem komputera powinno być podejściem naturalnym dla dzieci i młodzieży, jakże dobrze obeznanymi z nowoczesnymi technologiami. Ponadto może zaciekawić uczniów i umożliwia pobudzenie trzech dominujących zmysłów.
Przykładowe programy
W poniższym paragrafie przestawiono przykładowe programy przygotowane przez autorkę artkułu.
Program I: Działania na liczbach naturalnych – dodawanie
(Podstawa programowa: Działania na liczbach naturalnych. Uczeń: dodaje i odejmuje w pamięci liczby naturalne dwucyfrowe lub większe, liczbę jednocyfrową dodaje do dowolnej liczby naturalnej i odejmuje od dowolnej liczby naturalnej).
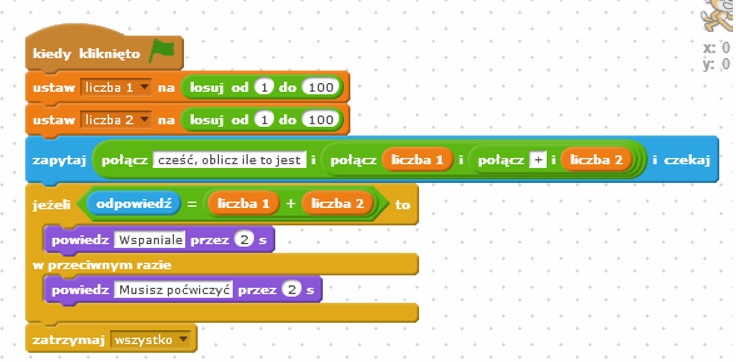
Celem poniższego programu jest utrwalenie wiedzy w zakresie dodawania w pamięci liczb naturalnych w zakresie od 1 do 100. Po uruchomieniu program wygeneruje i pokaże dwie liczby z powyższego zakresu. W kolejnym kroku uczeń zostanie poproszony o podanie wyniku obliczeń w pamięci. W przypadku podania przez ucznia prawidłowego wyniku program wyświetli komunikat Wspaniale przez 2 sekundy i się zatrzyma. Natomiast w przypadku uzyskania nieprawidłowej odwiedzi zostanie wyświetlony komunikat Musisz poćwiczyć również przez czas 2 sekund. Zarówno czasy wyświetlania komunikatów oraz ich treść może zostać zmieniona. Algorytm poniższy może bardzo łatwo zmodyfikować np. poprzez zmniejszenie zakresu liczb czy zwiększenie zakresu liczb do obliczeń, w zależności od poziomu uczniów. Ponadto program można bardzo prosto zmodyfikować zmieniając dodawanie na odejmowanie czy mnożenie lub dzielenie.
Rys 1) Przykładowy program dodawanie liczb w zakresie od 1 do 100.
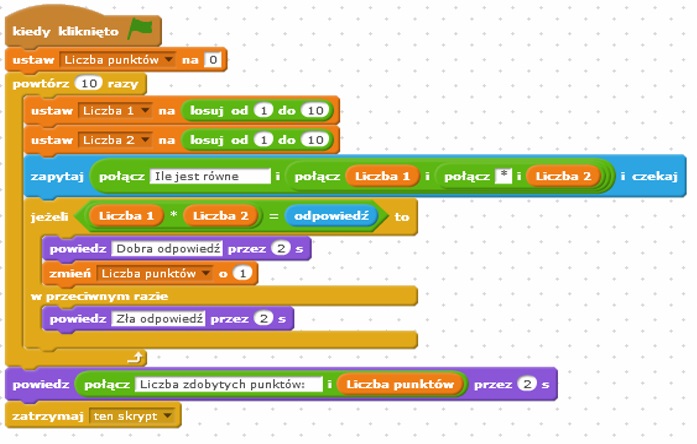
Program II: Działania na liczbach naturalnych – mnożenie (Podstawa programowa: Działania na liczbach naturalnych. Uczeń: mnoży i dzieli liczbę naturalną przez liczbę naturalną jednocyfrową, dwucyfrową lub trzycyfrową sposobem pisemnym, w pamięci (w najprostszych przykładach) i za pomocą kalkulatora (w trudniejszych przykładach).
Celem poniższego programu jest doskonalenie wiedzy w zakresie mnożenia w pamięci liczb naturalnych w zakresie od 1 do 100 w cyklu dziesięciu powtórzeń. Po uruchomieniu programu licznik punktów zostanie wyzerowany. Następnie program wygeneruje losowo pierwszą i drugą liczbę z zakresu od 1 -10. Wylosowane liczby zostaną wyświetlone odpowiednio w okienku liczba 1 oraz liczba 2. Kolejno skrypt wyświetli pytanie „Ile jest równe liczba 1* liczba 2” i poczeka na podanie wyniku działania przez ucznia. Jeśli uzyskana odpowiedź będzie prawidłowa zostanie wyświetlony, przez 2 sekundy, komunikat Dobra odpowiedź i przyznany jeden punkt uczniowi. Natomiast w przypadku wpisanie przez ucznia nieprawidłowej odwiedzi zostanie wyświetlony komunikat Zła odpowiedz. Licznik punktów nie zostaje w tym przypadku zwiększony. Następnie zostanie wyświetlony komunikat z aktualnie uzyskaną liczbą punktów. Po czym program wróci do początku i powtórzy całość algorytmy kolejne 9 razy.
Podobnie jak w przypadku pierwszego przedstawionego programu również w tym czasy wyświetlania komunikatów oraz ich treści może dowolnie zmieniać. Algorytm poniższy może bardzo łatwo zmodyfikować poprzez zwiększenie zakresu liczb branych do obliczeń czy ilości powtórzeń. Program może bardzo prosto, przez zmianę formuły, dostosować do ćwiczenia dzielenia.
Rys 2) Przykładowy program -Tabliczka mnożenia.
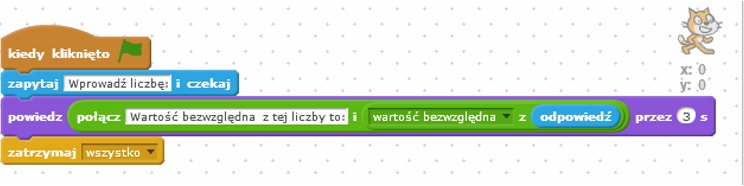
Program III: Działania na liczbach naturalnych – obliczanie wartości bezwzględnej
(Podstawa programowa: Liczby całkowite. Uczeń: oblicza wartość bezwzględną).
W opisanym poniżej przykładzie uczeń ćwiczy obliczanie wartości bezwzględnej. Algorytm jest bardzo prosty, po uruchomieniu użytkownik zostanie poproszony o podanie liczby. Następnie, program obliczy i wyświetli wartość bezwzględną do podanej wcześniej liczby.
Rys 3) Przykładowy program – obliczanie wartości bezwzględnej
Program IV: Działania na ułamkach dziesiętnych
(Podstawa programowa: Ułamki zwykłe i dziesiętne. Uczeń: zaokrągla ułamki dziesiętne).
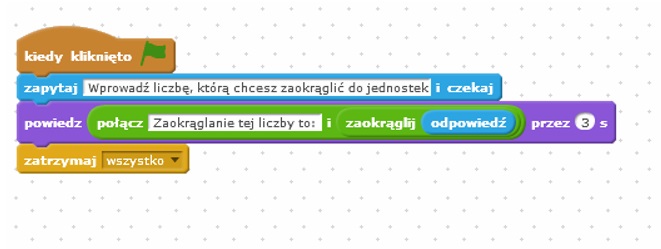
W opisanym poniżej, prostym programie uczeń będzie ćwiczył zaokrąglanie ułamków dziesiętnych. Program po uruchomieniu poprosi o podanie liczby – ułamka dziesiętnego. Następnie, po jej podaniu, wyświetli wyniki zaokrąglenia ułamka do jednostek.
Rys 4) Przykładowy program zaokrąglanie ułamków dziesiętnych.
Program V: Rysowanie kwadratu, własności kwadratu
(Podstawa programowa: Wielokąty, koła. Uczeń: rozpoznaje i nazywa: kwadrat, prostokąt, romb, równoległobok i trapez)
Celem poniższego programu jest doskonalenie wiedzy z zakresie geometrii w aspekcie rozpoznawania i nazywania figur: kwadrat, prostokąt, romb, równoległobok i trapez.
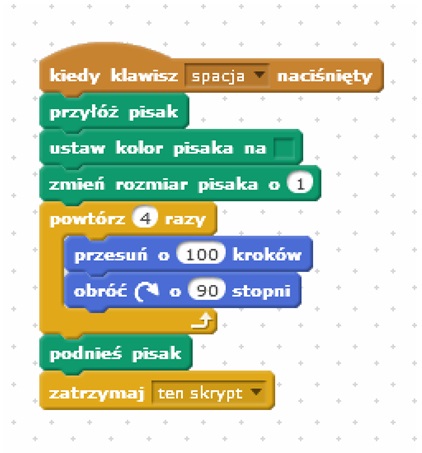
Po uruchomieniu programu, poprzez naciśniecie przycisku spacji, następuję wybranie pisaka oraz jego koloru, w tym przypadku zielonego jak również grubości linii, tu wybrana grubość linii to 1. Następnie algorytm wyrysuje na ekranie figurę kwadrat. Uczeń poprzez zmianę: kąta, ilości powtórzeń może wyrysować trójka lub wielokąt foremny. Zmieniając ilość kroków użytkownik wpływa na wielkość rysowanej figury a poprzez zmianę koloru czy grubości linii może wpływać na aspekty wizualne kreślonego wielokąta.
Rys 5) Przykładowy program – rysowanie kwadratu i jego własności
Program VI oblicza obwód wielokąta o danych długościach boków
(Podstawa programowa: Obliczenia w geometrii. Uczeń: oblicza obwód wielokąta o danych długościach boków)
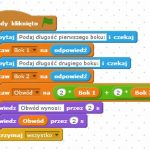
W opisanym niżej program pomaga uczniowi obliczyć obwód wielokątów o zadanej długości boków. Po uruchomieniu skryptu użytkownik zostanie poproszony o podanie długości pierwszego i następnie drugiego boku. W dalszej kolejności po wyświetleniu długości obu boków zostanie obliczony obwód figury i wyświetlony jego wartość.
Rys 6) Przykładowy program – oblicza obwód wielokąta o danych długościach boków.
Program VII: Obliczanie pola kwadratu.
(Podstawa programowa: Obliczenia w geometrii. Uczeń: oblicza obwód wielokąta o danych długościach boków).
Ostatni prezentowany programów wspiera ucznia w obliczaniu pola kwadratu. Po uruchomieniu programu zostanie wyświetlona informacja jakiej figury będzie obliczał pole i wylosowana długości boku z zakresu od 1-10. Następnie wyświetli wygenerowaną wielkość i poprosi ucznia o podanie obliczonego przez niego pola figury. W następnym kroku pokaże kolejno wynik obliczeń ucznia oraz dokonanych przez algorytm. W zależności czy wynik ucznia był poprawny wyświetli komunikat Świetnie. Jeśli natomiast uczeń poda błędną odpowiedź zostanie wyświetlony napis Niestety, Musi się pouczyć! I
Rys 7) Przykładowy program oblicza pola figur takich jak: trójkąta, kwadrat, prostokąt, romb, równoległobok, trapez.
Lidia Ignasiak
Bibliografia:
Majewicz, P. (2012). Aktywizacja myślenia matematycznego uczniów o specjalnych potrzebach edukacyjnych. Pobrane z http://rep.up.krakow.pl/xmlui/bitstream/handle/11716/3111/05–Aktywizacja-myślenia-matematycznego
Szeremeta, R. (1994). Potrzeby i możliwości aktywizacji uczniów w procesie nauczania techniki Pobrane z https://repozytorium.ukw.edu.pl/bitstream/handle/item/4772/Potrzeby%20i%20mozliwosci%20aktywizacji%20uczniow%20w%20procesie%20nauczania%20techniki.pdf?sequence=1&isAllowed=y
Janowicz, M. (2009). Uczenie się-wybrane zagadnienia. Folia Pomeranae Universitatis Technologiae Stetinensis. Oeconomica, (56), 73-82.
Operacje myślenia dywergencyjnego (czyli rozbieżnego), takiego w którym musimy nauczyć dziecko szukania różnych dróg do rozwiązania problemu/zadania/projektu, cechuje wysoka sprawność zdolności produktywnych, które są bardzo przydatne w obecnym świecie. To operacje myślenia dywergencyjnego decydują o uzyskaniu jak największej liczby pomysłów. Dzieci mają naturalną potrzebę poszukiwania.
„ Tajemnice Pani Przyrody są na wyciągnięcie ręki…. a może ogonka?”
Warto wykorzystać te predyspozycje do tego, by już na etapie klas I-III szkoły podstawowej zaszczepić w nich zdolność do działania na wielu płaszczyznach. Rozwój myślenia „wielobiegunowego” (tego określenia, stworzonego prze siebie, lubię używać w praktyce pedagogicznej), w perspektywie czasu da umiejętność radzenia sobie w życiu dorosłym – w pracy, która będzie wymagała ciągłego rozwiązywania problemów, presji czasu, przy jednoczesnej swobodzie myślenia. Do najważniejszych zdolności myślenia dywergencyjnego należą: płynność, giętkość, oryginalność. Płynność myślenia polega na zdolności do szybkiego i swobodnego posługiwania się słowami, obrazami, wyobrażeniami dźwiękowymi, w zależności od problemu. Zdolność nazywana płynnością skojarzeniową ułatwia wytwarzanie skojarzeń obrazowych, ruchowych, dźwiękowych, słownych.
„Zielono mi …śpiewam, tańczę, recytuję…. i w tym wszystkim swobodę czuję …”
Zdolność ta decyduje o liczbie wysuwanych pomysłów zmierzających do konkretnego rozwiązania zadania. Giętkość myślenia natomiast umożliwia wytwarzanie jakościowe różnych rozwiązań, ułatwia zejście z błędnej drogi poszukiwania. Oryginalność ułatwia wytwarzanie nieprzeciętnych pomysłów rozwiązania.
„Dodać STWORZENIU skrzydeł, by wzlecieć ponad przeciętność…”
Zdolności myślenia dywergencyjnego decydują w dużym stopniu o twórczym charakterze intelektu człowieka, stanowią podstawę myślenia twórczego. Ważnym elementem w rozwoju myślenia dywergencyjnego są operacje oceny. Ocenianie polega na umiejętności wydawania sądów wartościujących dotyczących np. poprawności, przydatności, oryginalności, odczuwania wartości. Umiejętność orzekania o poprawności i użyteczności wymaga wielu elementarnych zdolności. Już Guilford (amerykański psycholog, pedagog i statystyk) nazywa je łącznie „wrażliwością na problemy”. Z praktyki wynika, że dziecku, któremu udało się wymyślić coś twórczego, czuje się lepsze, mądrzejsze, co samo w sobie jest wartością. I wcale dziecko myślące dywergencyjnie nie musi być nadzwyczaj uzdolnione. Miałam kolegę, który w podstawówce „nie grzeszył” nadmiarem posiadanej wiedzy. Jednak swoje działania opierał na sprycie, wymyślaniu różnych rozwiązań, niekoniecznie i nie zawsze słusznych. Efekt końcowy jego wojaży natomiast zawsze kończył się sukcesem. Obecnie ma bardzo dobrze prosperującą firmę, zatrudnia wielu ludzi… Po latach, gdy się spotykamy, dochodzimy do takich samych wniosków. Dawniej nie znałam pojęcia myślenia dywergencyjnego, jednak intuicyjnie śledząc dokonania kolegi, nazwałam sobie ten proces „umiejętnością patrzenia więcej niż jedną parą oczu”. Takich osób było sporo w moim życiu… Osób, które poszukiwały czegoś więcej niż wiedzy lub czegoś zamiast wiedzy. I jedni i drudzy mają na chwilę obecną niezłe wyniki w swej pracy zawodowej. Rozpoczynając moją przygodę życia w Szkole Podstawowej w Kosarzyskach (15 lat temu), postanowiłam zrobić „coś” więcej niż tylko przekazywać wiedzę oraz zrobić „coś” dla tych, których potencjał intelektualny niekoniecznie pozwala na zdobywanie piątek i szóstek. Tym „czymś” było wdrożenie Innowacji Pedagogicznej pt. „ Schodami do kreatywności”, która miała początkowo na celu uprzyjemnić zajęcia, wprowadzić więcej swobody myślenia, podarować uczniom (wszystkim) możliwość wypowiedzenia się na dany temat bez wstawiania przysłowiowych pał za błędne w oczach nauczyciela myślenie. Nie było złych odpowiedzi. Każda miała swoją wartość wyższą bądź niższą, ale jednak wartość. Dało to moim dzieciom poczucie bezpieczeństwa – podczas wypowiadania się, zadawania pytań, później i tych w życiu dorosłym. Nie przerodziło się w zdobywanie pierwszych miejsc na olimpiadach, konkursach wiedzowych, intelektualnych sprawdzianach, ale dało gwarancje, że każde z tych dzieci o siebie potrafiło walczyć.
„Anielskie ognisko z wykorzystaniem kapeluszy myślowych….”
Już teraz z dumą obserwuję poczynania moich byłych uczniów, którzy w szkole podstawowej potrafili myśleć, myśleć twórczo, do tego dywergencyjnie. Podam przykład chłopca, który miał bardzo słabe oceny, wręcz cudem przechodził z klasy do klasy, bo oceniany był przede wszystkim za wiedzę, a raczej jej brak oraz pozostawiające wiele do życzenia zachowanie. Nie był lubiany, bo często uważany za przemądrzałego. W moich oczach natomiast pozostawał jako ten niepokorny, ale w dobrym tego słowa znaczeniu, szukający rozwiązania, konstruktywny, twórczy i śmiało mogę teraz określić go jako człowieka „dywergencyjnego”. Gdybym mogła, obserwując jego obecne poczynania, przydzieliłabym mu nagrodę „społecznika roku”, z niebanalnymi pomysłami na życie. I to jest duma. Owszem radość sprawiają w mym sercu także Marysie, Justynki, Anie, które były szóstkowe, są przykładne w dorosłym życiu, pokornie przyznają każdemu rację. Ale nie do końca jest to dla nich dobre. Rzeczywistość nasączona presją niszczy je. I szkoda, że od szkoły wymaga się tak naprawdę wyników, wyników, wyników za wiedzę… Szkoda… Wbrew temu postanowiłam po kilku latach napisać kolejną Innowację pedagogiczną, mającą na celu myślenie twórcze zawęzić właśnie głównie do tego dywergencyjnego, które w moim przekonaniu przełoży się na największe sukcesy w dojrzałym życie ucznia.
„Moje pomysły na przyszłość… Jestem Wielkim Człowiekiem, a będę jeszcze Większym ….”
Jakże byłam zniesmaczona, kiedy opowiadając (zresztą zapytana) podczas szkolenia o innowacjach o moich byłych i obecnych pomysłach, kiedy Pani prowadząca zapytała: „Czy Pani dokładnie monitorowała i monitoruje swoje programy i jak te innowacje przekładają się na oceny uczniów?” i lekceważące szemrania współuczestników szkolenia, „…że z wróbla orła nie zrobi”… Hmmm… Najważniejsze wyniki wyrażone w stopniach. Owszem, są one ważne, ale to nie wszystko. Czy przyszły pracodawca, podczas rozmowy kwalifikacyjnej, pyta o stopnie ze szkoły, czy raczej od razu położy nacisk na umiejętności, pomysły, jakość pracy i jej efektywność? Zwłaszcza w dużych korporacjach. Tak więc spokojnie i z optymizmem, mimo zgryźliwych uwag, rozpoczęłam w tym roku szkolnym, z moją obecnie pierwszą klasą Innowację pt. „Szukam rozwiązania zadania wielu dróg… Wybiorę najlepszą z nich, którą pójść bym mógł”. Moje oczekiwania po zakończeniu trzyletniej innowacji nie będą przekładały się na oceny. Będę dumna, gdy moi uczniowie, napotkani po latach na drodze, będą z dumą opowiadali o swoich dokonaniach, spełnionych marzeniach, osiągniętych celach. Innowacja przyniesie wtedy rezultat, gdy będą oni pracowali ze swobodą, lekkością, nie poddadzą się presji stresu i nacisku, znając swoją wartość i niepowtarzalność, nie mierzoną piątką czy szóstką ze sprawdzianu. Nie wystarczy być człowiekiem rozumnym, żeby być myślącym. Do tego „myślenie czasem wymaga planowego wysiłku” (Edward de Bono).
„Planując pracę w domowym zaciszu… również myślę dywergencyjnie…”
Nie zawsze można polegać na myśleniu spontanicznym, odruchowym. Często popełniamy błędy przy rozwijaniu zdolności myślenia. Dajemy dzieciom zadanie zbyt trudne do rozwiązania, które niszczą zaufanie do samego siebie. Dziecko zniechęca się do myślenia. Tak wiec nauczyciel musi być cały czas osobą motywującą. I wówczas myślenie jest przyjemne, bywa niemal zabawą. Dzieci w takich warunkach uwielbiają myśleć, korzystać z własnych nowinek. Musimy dać im szansę osiągania sukcesów.
„Inne spojrzenie na świat… niekoniecznie przez różowe okulary…”
Sukcesy w prawidłowym odgadywaniu budzą optymizm, wiarę we własne siły, co ma duże znaczenie w przygotowaniu dziecka do sprostowania obowiązkom szkolnym, a potem tych w dorosłym życiu. Rozwój nastawień twórczych u dzieci zależy od wprowadzenia nowych treści i rodzajów ćwiczeń oraz od wytwarzania w toku kształcenia specyficznej atmosfery. Jej twórcą jest w pierwszej kolejności nauczyciel, który sam powinien odznaczać się silną motywacją twórczą (myślę, że tę umiejętność w sobie wykształciłam). Jeżeli nauczyciel potrafi razem z uczniami szukać różnych rozwiązań tego samego problemu, wówczas wspólnie z nimi przeżywa radość twórczego poszukiwania i nie tylko aktywizuje ich intelektualnie, lecz kształci twórczy stosunek do życia, dodam twórczość dywergencyjną. Tak jak wspomniałam powyżej, dynamiczny rozwój cywilizacji wywiera coraz większą presję na nauczanie i wychowanie. Niestety w szkole polskiej nadal (mimo tego, że twierdzi się inaczej) nie są w dostatecznej mierze rozwijane twórcze procesy psychiczne. Metodami dominującymi są wciąż te oparte na przekazie słownym i zapamiętywaniu wiadomości. Można by powiedzieć, że proces nauczania sprowadza się do mówienia nauczyciela i słuchania przez uczniów tego, co przekazuje ich „mistrz”. Uczeń w takiej szkole jest niestety bierny. Jeśli jednak zależy nam na przygotowaniu dzieci do życia w rozwijającym się świecie, musimy zatroszczyć się o to, by szkoła dawała możliwość wprowadzenia nauczania myślenia twórczego, kreatywnego, dywergencyjnego. Mój autorski program nakierowany jest na takie nauczanie, które można rozpatrzeć w trzech aspektach. Po pierwsze, zastosowane metody i techniki (również stworzone przeze mnie) mają ośmielić ucznia do twórczości. Po drugie, pomóc w rozeznaniu indywidualnych zdolności twórczych i po trzecie: wspierać kreatywność ucznia. Treści programu mają charakter spiralny, który jest przydatny zwłaszcza w nauczaniu uczniów w młodszym wieku szkolnym. Taki układ daje możliwość wielokrotnego powrotu do poznanych już treści, lecz w bardziej rozwiniętej formie, zgodnie ze wzrastającymi możliwościami intelektualno- percepcyjnymi. W niewielkiej części program ma również budowę liniową, a utrwalanie i rozszerzanie danej treści przewidywane jest w klasach starszych szkoły podstawowej. Podczas zajęć dzieci mają możliwość pracowania zarówno samodzielnie, jak i grupowo. Program opiera się na modelu hermeneutycznym, traktującym wiedzę jako produkt współtworzenia, którego dokonują wspólnie uczniowie i nauczyciel. Taki model koncentruje się na odpowiedzi na pytanie: jak współtworzyć świat? Nawiązując do pragmatyzmu pedagogicznego, preferuje uczenie się poprzez doświadczenie i działanie. Proces uczenia się sprowadzony jest do procesu badawczego. Głównym wyznacznikiem programu stymulowania myślenia dywergencyjnego na etapie nauczania początkowego jest specyfika tego etapu kształcenia, jak również wiek ucznia. Jest to bowiem okres wzmożonego rozwoju i kształtowania się podstawowych wiadomości, umiejętności i twórczych procesów psychicznych. Program je eksponuje, podporządkowując im treści z różnych dziedzin edukacji. Cele są formułowane w sposób ogólny i dotyczą całego etapu kształcenia w klasach I-III. Nadrzędnym celem jest wspomaganie wszechstronnego i harmonijnego rozwoju ucznia. Cele szczegółowe odnoszą się do zamierzonych efektów pracy i mają charakter operacyjny. Te szczegółowe umiejętności są bazą tworzenia umiejętności wyższego rzędu, to znaczy :
Uczenie się.
Myślenie.
Poszukiwanie.
Doskonalenie się.
Komunikowanie się..
Współpraca.
Działanie.
„Nagrałem film o moim Tatusiu….”
Hasła programowe pokazują, jakie podstawowe umiejętności powinien nabyć uczeń w trakcie realizacji zajęć. Program ma na celu:
Stymulowanie u uczniów twórczego myślenia.
Mobilizowanie uczniów do kreatywnego, dywergencyjnego myślenia.
Rozwijanie umiejętności wyrażania uczuć (pozytywnych, negatywnych) za pomocą słów, gestów i mimiki.
Cele operacyjne tworzą przewidywane osiągnięcia uczniów. Dziecko w toku trwania innowacji (oraz po jej zakończeniu w życiu codziennym):
poda nowatorskie pomysły,
oceni pomysły swoje i innych,
wyrazi własne myśli i odczucia,
dokona wyboru pomiędzy tym co ważne i mniej ważne,
poszuka optymalnych, twórczych rozwiązań,
rozwinie swoją wyobraźnię,
wykona nowatorskie prace z zakresu sztuki: muzyka, plastyka,
pokona onieśmielenie,
dostrzeże własną wartość,
wyeksponuje swoje różnorodne zdolności,
dokona próby obrony własnego zdania,
przedstawi swoje poglądy i przekonania,
krytycznie spojrzy na własne poglądy i je zweryfikuje,
uważnie wysłucha innych,
dokona samooceny i oceny pracy w grupie,
podejmie decyzję,
odegra scenki dramowe,
wyrazi uczucia za pomocą mimiki i gestów,
twórczo zaplanuje spędzanie wolnego czasu,
zaplanuje kolejne etapy pracy,
wybierze najlepsze propozycje,
dokona analizy i syntezy,
przeprowadzi rozmowy lub wywiady,
ułoży dalszą część wypowiedzi,
ułoży rozsypanki,
przeczyta cicho teksty ze zrozumieniem,precyzyjnie zredaguje polecenia,
wykona piramidę priorytetów,
wykorzysta różne źródła wiedzy,
pozna nowe sposoby szybkiego gromadzenia treści,
skorzysta z posiadanych wiadomości,
wspólnie z innymi opracuje podany materiał,
wypowie się precyzyjnie na określony temat,
wykaże się aktywnością w pracy grupowej.
By zachować integralność z podstawą programową, w innowacji wzięto pod uwagę cele kształcenia i wychowania w nauczaniu:
wprowadzenie do procesu nauczania elementów zabawy,
wspomaganie wszechstronnego i harmonijnego rozwoju ucznia,
atrakcyjne wprowadzanie i utrwalanie treści programowych z zastosowaniem metod i technik aktywizujących,
rozwijanie samodzielności i logicznego myślenia,
pobudzanie do samodzielnej i twórczej pracy,
wyrabianie pozytywnych postaw społecznych,
kształtowanie umiejętności porozumiewania się z rówieśnikami i dorosłymi w różnych sytuacjach,
rozwijanie podstawowych umiejętności służących świadomemu uczeniu się,
pomaganie w kształtowaniu pozytywnego obrazu samego siebie oraz rozpoznawać i nazywać własne i cudze uczucia,
wdrażanie do czynnego uczestniczenia w życiu społeczeństwa.
„Myśleć twórczo- to nie bać się ani wzburzonych fal, ani stromych gór… To iść pod prąd z własnymi pomysłami mimo wszystko…”
Zachęcam wszystkich twórczych nauczycieli do odwagi w podejmowaniu działań innowacyjnych i nie poddaniu się stereotypom związanym z nauczaniem. Powodzenia.
Małgorzata Rams
Małgorzata Rams to nauczyciel dyplomowany z 15-letnim stażem; wykładowca na studiach podyplomowych, głównie pedagogicznych. Pracuje w placówkach oświatowych. Współpracuje z placówkami medycznymi, prowadząc terapię logopedyczną dla osób starszych po hospitalizacji. Prowadzi prywatny Gabinet Logopedyczno-Pedagogiczny (diagnoza i terapia dzieci, młodzieży i dorosłych). Pasjonatka wykonywanego zawodu. Stale się dokształca (ukończyła ponad 100 różnych form doskonalenia). Posiada wykształcenie jako: Logopeda; Oligofrenopedagog; Nauczyciel (pedagogika przedszkolna i wczesnoszkolna; nauczanie początkowe z wychowaniem muzycznym). Ponadto ukończyła: Studia z organizacji i zarządzania oświatą ; studia w zakresie ICT, języków obcych oraz drugiego przedmiotu: „Przygotowanie do życia w rodzinie”.
Prezentujemy czwarty i ostatni konspekt zajęć z języka angielskiego autorstwa pani nauczycielki Agaty. Zajęcia przygotowano dla uczniów szkół podstawowych i dotyczą sposobów wykorzystania Internetu i komputera do nauki języka obcego. Temat czwarty: Christmas quizzes on Kahoot.
Prezentujemy trzeci konspekt zajęć z języka angielskiego autorstwa pani nauczycielki Agaty. Zajęcia przygotowano dla uczniów szkół podstawowych i dotyczą sposobów wykorzystania Internetu i komputera do nauki języka obcego. Temat trzeci: Emoticon’s crossword puzzles.
Prezentujemy drugi konspekt zajęć z języka angielskiego autorstwa pani nauczycielki Agaty. Zajęcia przygotowano dla uczniów szkół podstawowych i dotyczą sposobów wykorzystania Internetu i komputera do nauki języka obcego. Temat drugi: Postcards from holidays.
Prezentujemy konspekt zajęć z języka angielskiego autorstwa pani nauczycielki Agaty. Zajęcia przygotowano dla uczniów szkół podstawowych i dotyczą sposobów wykorzystania Internetu i komputera do nauki języka obcego. Temat pierwszy: The weather around the world.
