W poniższym artykule przedstawiono propozycję wykorzystania programów przygotowanych przy pomocy programu Scratch do wspierania aktywnego procesu nauczania i utrwalania wiedzy w zakresie matematyki.
Co to jest aktywizacja
Jak wskazuje Majewicz(2012) słowa „aktywność” oraz „aktywizacja” wywodzą się od tego samego łacińskiego słowa activus oznaczającego czynny. Zatem aktywizacje uczniów można rozumieć jako proces, którego celem jest doprowadzenie do sytuacji, w której uczniowie aktywnie uczestniczą w procesie nauczania i zdobywania nowej wiedzy. Aktywizacja jest też określana jako ogół poczynań nauczyciela i uczniów zapewniających dzieciom odgrywanie czynnej roli w realizacji zadań. Uczniowie uczą się w trakcie własnej aktywności. Chodzi o to, by potrzebną wiedzę i umiejętności nabywali w sposób trwały, skuteczny i przyjemny.
Dlaczego aktywizacja i porównanie
W nauczaniu matematyki często, historycznie stosowane były metody podające, ponieważ dawniej uczenie się polegało prawie wyłącznie na przyswajaniu gotowej wiedzy. Obecnie dydaktyka daje pierwszeństwo metodom problemowym ze szczególnym uwzględnieniem metod aktywizujących. Kładzie się na nacisk na kształtowanie postawy uczniów wobec poznawanych zagadnień. Kluczowa rola takiego podejścia wynika z powiązania z rzeczywistością pozą szkolną, której odkrywania realizuje się przede wszystkim poprzez działanie, a także ze względu na skuteczność (Szeremeta, 1992). Propagatorzy metod aktywizujących zwracają uwagę na samodzielne dochodzenie uczniów do wiedzy, co powoduje, że staje się ona bardziej trwała, a także zaangażowanie w takiej lekcji wszystkich uczniów pogłębia ich zdolności pracy w grupie oraz możliwości analizowania i interpretowanie rzeczywistości. Należy pamiętać, że umiejętności te są kluczowe we współczesnym świecie.
Różnorodność aktywności a mimo to skuteczność
Aktywność uczniów może przejawiać się w odmiennych formach i w różnym nasileniu. Wynika to między innymi z tego, że różne zmysły mogą w mniejszym lub większym stopniu wpływać na przyswajanie wiedzy u konkretnego dziecka. Wyróżnia się wzrokowców, słuchowców i kinestetyków w zależności od tego, czy dominującym zmysłem jest odpowiednio wzrok, słuch lub dotyk oraz czynności ruchowe (Janowicz, 2009). Metody aktywizujące także te zaprezentowane jako konkretne przykłady można uznać za obiektywne, w takim sensie, że dostarczają bodźców do tych trzech dominujących zmysłów. Ponadto niezależnie od sposobu przyswajania informacji przez konkretnego ucznia, metoda przyjęta przez nauczyciela może radykalnie zmienić ilość przyswojonych informacji. W poniższych przykładach zamiast podawać gotowe informacje (uczniowie pamiętają tylko 10% z tego, co słyszą i/lub widzą), nauczyciel zachęca uczniów i daje warunki do bycia odkrywcą i eksperymentatorem, wprowadzenie atrakcyjnych środków dydaktycznych działających na wzrok powoduje już wzrost zapamiętywania informacji do 20%. Idąc dalej umożliwienie uczniom możliwości rozmowy i dyskusji, o swoich programach, zwiększa ilość zapamiętywanej informacji do 40%. Na koniec umożliwienie uczniom uczenia się poprzez działanie, opracowanie własnego programu, powoduje iż zapamiętują 90% tego, co robią.
Narzędzia informatyczne
Poniższe przekłady stanowią propozycję wykorzystanie narzędzi informatycznych do rozwiania u uczniów umiejętności matematycznych. Rozwiazywanie problemu z wykorzystaniem komputera powinno być podejściem naturalnym dla dzieci i młodzieży, jakże dobrze obeznanymi z nowoczesnymi technologiami. Ponadto może zaciekawić uczniów i umożliwia pobudzenie trzech dominujących zmysłów.
Przykładowe programy
W poniższym paragrafie przestawiono przykładowe programy przygotowane przez autorkę artkułu.
Program I: Działania na liczbach naturalnych – dodawanie
(Podstawa programowa: Działania na liczbach naturalnych. Uczeń: dodaje i odejmuje w pamięci liczby naturalne dwucyfrowe lub większe, liczbę jednocyfrową dodaje do dowolnej liczby naturalnej i odejmuje od dowolnej liczby naturalnej).
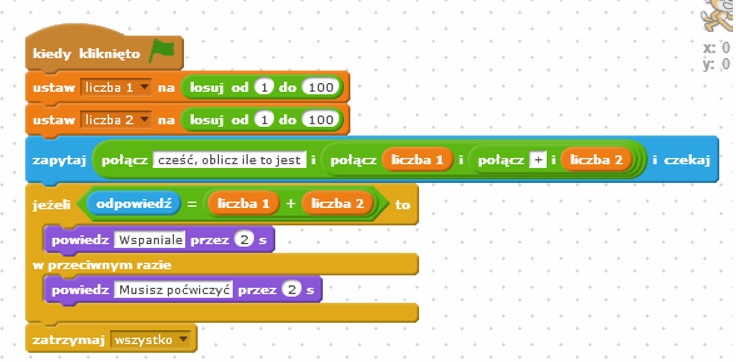
Celem poniższego programu jest utrwalenie wiedzy w zakresie dodawania w pamięci liczb naturalnych w zakresie od 1 do 100. Po uruchomieniu program wygeneruje i pokaże dwie liczby z powyższego zakresu. W kolejnym kroku uczeń zostanie poproszony o podanie wyniku obliczeń w pamięci. W przypadku podania przez ucznia prawidłowego wyniku program wyświetli komunikat Wspaniale przez 2 sekundy i się zatrzyma. Natomiast w przypadku uzyskania nieprawidłowej odwiedzi zostanie wyświetlony komunikat Musisz poćwiczyć również przez czas 2 sekund. Zarówno czasy wyświetlania komunikatów oraz ich treść może zostać zmieniona. Algorytm poniższy może bardzo łatwo zmodyfikować np. poprzez zmniejszenie zakresu liczb czy zwiększenie zakresu liczb do obliczeń, w zależności od poziomu uczniów. Ponadto program można bardzo prosto zmodyfikować zmieniając dodawanie na odejmowanie czy mnożenie lub dzielenie.
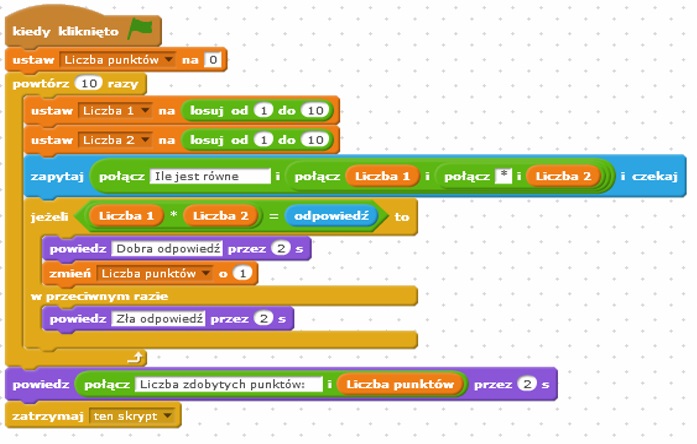
Program II: Działania na liczbach naturalnych – mnożenie
(Podstawa programowa: Działania na liczbach naturalnych. Uczeń: mnoży i dzieli liczbę naturalną przez liczbę naturalną jednocyfrową, dwucyfrową lub trzycyfrową sposobem pisemnym, w pamięci (w najprostszych przykładach) i za pomocą kalkulatora (w trudniejszych przykładach).
Celem poniższego programu jest doskonalenie wiedzy w zakresie mnożenia w pamięci liczb naturalnych w zakresie od 1 do 100 w cyklu dziesięciu powtórzeń. Po uruchomieniu programu licznik punktów zostanie wyzerowany. Następnie program wygeneruje losowo pierwszą i drugą liczbę z zakresu od 1 -10. Wylosowane liczby zostaną wyświetlone odpowiednio w okienku liczba 1 oraz liczba 2. Kolejno skrypt wyświetli pytanie „Ile jest równe liczba 1* liczba 2” i poczeka na podanie wyniku działania przez ucznia. Jeśli uzyskana odpowiedź będzie prawidłowa zostanie wyświetlony, przez 2 sekundy, komunikat Dobra odpowiedź i przyznany jeden punkt uczniowi. Natomiast w przypadku wpisanie przez ucznia nieprawidłowej odwiedzi zostanie wyświetlony komunikat Zła odpowiedz. Licznik punktów nie zostaje w tym przypadku zwiększony. Następnie zostanie wyświetlony komunikat z aktualnie uzyskaną liczbą punktów. Po czym program wróci do początku i powtórzy całość algorytmy kolejne 9 razy.
Podobnie jak w przypadku pierwszego przedstawionego programu również w tym czasy wyświetlania komunikatów oraz ich treści może dowolnie zmieniać. Algorytm poniższy może bardzo łatwo zmodyfikować poprzez zwiększenie zakresu liczb branych do obliczeń czy ilości powtórzeń. Program może bardzo prosto, przez zmianę formuły, dostosować do ćwiczenia dzielenia.
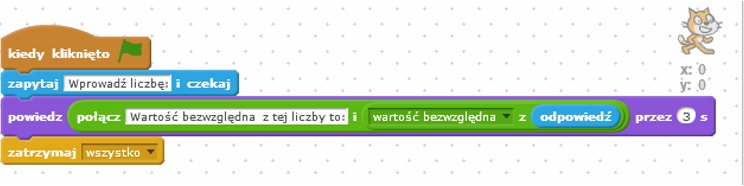
Program III: Działania na liczbach naturalnych – obliczanie wartości bezwzględnej
(Podstawa programowa: Liczby całkowite. Uczeń: oblicza wartość bezwzględną).
W opisanym poniżej przykładzie uczeń ćwiczy obliczanie wartości bezwzględnej. Algorytm jest bardzo prosty, po uruchomieniu użytkownik zostanie poproszony o podanie liczby. Następnie, program obliczy i wyświetli wartość bezwzględną do podanej wcześniej liczby.
Program IV: Działania na ułamkach dziesiętnych
(Podstawa programowa: Ułamki zwykłe i dziesiętne. Uczeń: zaokrągla ułamki dziesiętne).
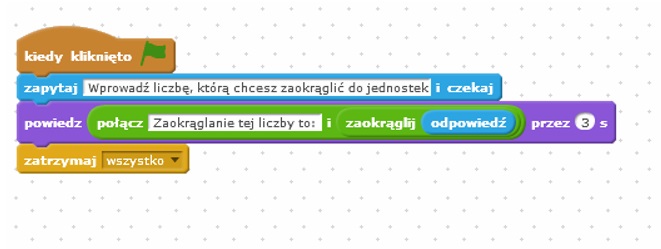
W opisanym poniżej, prostym programie uczeń będzie ćwiczył zaokrąglanie ułamków dziesiętnych. Program po uruchomieniu poprosi o podanie liczby – ułamka dziesiętnego. Następnie, po jej podaniu, wyświetli wyniki zaokrąglenia ułamka do jednostek.
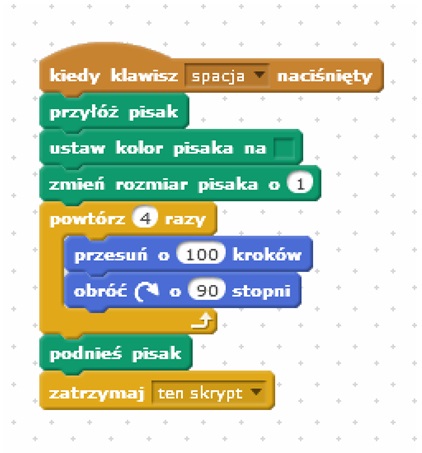
Program V: Rysowanie kwadratu, własności kwadratu
(Podstawa programowa: Wielokąty, koła. Uczeń: rozpoznaje i nazywa: kwadrat, prostokąt, romb, równoległobok i trapez)
Celem poniższego programu jest doskonalenie wiedzy z zakresie geometrii w aspekcie rozpoznawania i nazywania figur: kwadrat, prostokąt, romb, równoległobok i trapez.
Po uruchomieniu programu, poprzez naciśniecie przycisku spacji, następuję wybranie pisaka oraz jego koloru, w tym przypadku zielonego jak również grubości linii, tu wybrana grubość linii to 1. Następnie algorytm wyrysuje na ekranie figurę kwadrat. Uczeń poprzez zmianę: kąta, ilości powtórzeń może wyrysować trójka lub wielokąt foremny. Zmieniając ilość kroków użytkownik wpływa na wielkość rysowanej figury a poprzez zmianę koloru czy grubości linii może wpływać na aspekty wizualne kreślonego wielokąta.
Rys 5) Przykładowy program – rysowanie kwadratu i jego własności
Program VI oblicza obwód wielokąta o danych długościach boków
(Podstawa programowa: Obliczenia w geometrii. Uczeń: oblicza obwód wielokąta o danych długościach boków)
W opisanym niżej program pomaga uczniowi obliczyć obwód wielokątów o zadanej długości boków. Po uruchomieniu skryptu użytkownik zostanie poproszony o podanie długości pierwszego i następnie drugiego boku. W dalszej kolejności po wyświetleniu długości obu boków zostanie obliczony obwód figury i wyświetlony jego wartość.
Program VII: Obliczanie pola kwadratu.
(Podstawa programowa: Obliczenia w geometrii. Uczeń: oblicza obwód wielokąta o danych długościach boków).
Ostatni prezentowany programów wspiera ucznia w obliczaniu pola kwadratu. Po uruchomieniu programu zostanie wyświetlona informacja jakiej figury będzie obliczał pole i wylosowana długości boku z zakresu od 1-10. Następnie wyświetli wygenerowaną wielkość i poprosi ucznia o podanie obliczonego przez niego pola figury. W następnym kroku pokaże kolejno wynik obliczeń ucznia oraz dokonanych przez algorytm. W zależności czy wynik ucznia był poprawny wyświetli komunikat Świetnie. Jeśli natomiast uczeń poda błędną odpowiedź zostanie wyświetlony napis Niestety, Musi się pouczyć! I

Lidia Ignasiak
Bibliografia:
Majewicz, P. (2012). Aktywizacja myślenia matematycznego uczniów o specjalnych potrzebach edukacyjnych. Pobrane z http://rep.up.krakow.pl/xmlui/bitstream/handle/11716/3111/05–Aktywizacja-myślenia-matematycznego
Szeremeta, R. (1994). Potrzeby i możliwości aktywizacji uczniów w procesie nauczania techniki Pobrane z https://repozytorium.ukw.edu.pl/bitstream/handle/item/4772/Potrzeby%20i%20mozliwosci%20aktywizacji%20uczniow%20w%20procesie%20nauczania%20techniki.pdf?sequence=1&isAllowed=y
Janowicz, M. (2009). Uczenie się-wybrane zagadnienia. Folia Pomeranae Universitatis Technologiae Stetinensis. Oeconomica, (56), 73-82.